
안녕하세요! 개발감자입니다.
오늘 이진트리의 핵심이론과 이진트리를 순회하는 방법에 이야기해볼게요.
이진트리를 알아보기에 앞서 트리의 개념이 헷갈리는 분이 계신다면, 아래의 포스팅을 참고하시길 바랍니다.
[알고리즘 마스터] 14. 트리와 트라이
안녕하세요! 개발감자입니다🥔 오늘은 알고리즘 중 트리와 트라이에 대해서 정리하고 백준 문제를 통해 구현해보는 시간을 가져보도록 하겠습니다. 1. 트리 알아보기 트리는 그래프의 특수한
qkrrmsdud.tistory.com
1. 이진 트리의 개념
이진 트리(Binary Tree)는 각 노드가 최대 두 개의 자식 노드를 가지는 트리 구조를 말합니다. 각 노드는 부모 노드와 왼쪽 자식 노드, 오른쪽 자식 노드를 가질 수 있습니다. 이진 트리는 데이터 검색, 정렬, 계층 구조 등 다양한 알고리즘에서 활용됩니다.
이진 트리의 주요 특징은 다음과 같습니다:
- 각 노드는 최대 두 개의 자식 노드를 가질 수 있음.
- 왼쪽 서브 트리의 모든 노드는 해당 노드보다 작은 값을 가지며, 오른쪽 서브 트리의 모든 노드는 해당 노드보다 큰 값을 갖음.
2. 이진트리의 종류
이진 트리는 여러 종류가 있으며, 주요한 종류는 다음과 같습니다.
2-1. 편향 이진 트리 (Skewed Binary Tree)

편향 이진 트리는 모든 노드가 왼쪽 또는 오른쪽 서브 트리로만 존재하는 트리입니다. 이는 특정 노드를 기준으로 한쪽으로 치우쳐져 있어서 트리의 높이가 매우 큰 상태를 나타냅니다. 이러한 편향은 데이터의 삽입 순서에 따라 발생할 수 있으며, 이 경우 트리의 성능이 일반적인 이진 트리와 비교하여 나빠질 수 있습니다. 탐색 속도가 저하되고 공간이 많이 낭비되게 됩니다.
2-2. 포화 이진 트리 (Full Binary Tree)

포화 이진 트리는 모든 레벨이 꽉 차 있는 이진 트리입니다. 즉, 각 노드가 0개 또는 2개의 자식 노드를 가지며, 모든 레벨에 노드가 꽉 차 있는 상태를 말합니다. 포화 이진 트리는 노드들 간의 균형이 잘 잡혀 있어 검색과 정렬 작업에 효과적입니다. 하지만 노드의 수가 2^n - 1로 고정되어 있어 모든 레벨이 꽉 차 있지 않을 경우에는 포화 이진 트리가 아닙니다.
2-3. 완전 이진 트리 (Complete Binary Tree)

완전 이진 트리는 마지막 레벨을 제외한 모든 레벨이 완전히 채워져 있고, 마지막 레벨의 노드는 왼쪽부터 차례대로 채워진 트리입니다. 이 특성 때문에 배열을 사용하여 효율적으로 구현할 수 있습니다. 완전 이진 트리는 힙(heap) 자료구조를 구현할 때 주로 사용되며, 레벨순회(level order traversal)와 같은 알고리즘에 유용합니다.
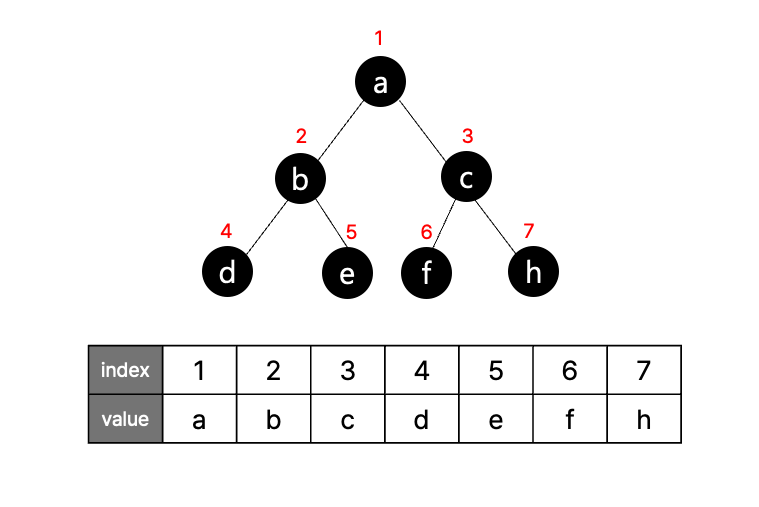
2-4. 이진트리 1차원 리스트로 표현하기
아래와 같이 1차원 리스트의 형태로 표현할 수 있습니다.
3. 이진트리 순회
이진 트리를 순회하는 방법에는 세 가지 주요 방법이 있습니다:
- 전위 순회(Preorder Traversal) : 노드를 왼쪽 서브 트리부터 시작하여 루트, 왼쪽, 오른쪽 순으로 방문합니다.
- 중위 순회(Inorder Traversal) : 노드를 왼쪽 서브 트리, 루트, 오른쪽 서브 트리 순으로 방문합니다. 이 방법은 BST에서 정렬된 순서로 노드를 출력합니다.
- 후위 순회(Postorder Traversal) : 노드를 왼쪽 서브 트리, 오른쪽 서브 트리, 루트 순으로 방문합니다. 리프 노드부터 시작하여 거꾸로 올라오는 방식입니다.
4. 이진트리 응용하기
백준 문제 1991번 트리 순회하기를 보면서 이진트리를 코딩테스트에서 어떻게 응용하는지 함께 보실까요?
import sys
input = sys.stdin.readline
# 입력
n = int(input())
tree = {}
for i in range(n):
root,left,right = map(str, input().split()) #현재 노드, 왼쪽 노드, 오른쪽 노드
tree[root] = [left, right]
def preOrder(now):
if now == '.':
return
print(now,end='')
preOrder(tree[now][0]) # 왼쪽 탐색
preOrder(tree[now][1]) # 오른쪽 탐색
def inOrder(now):
if now == '.':
return
inOrder(tree[now][0]) # 왼쪽 탐색
print(now,end='')
inOrder(tree[now][1]) # 오른쪽 탐색
def postOrder(now):
if now == '.':
return
postOrder(tree[now][0]) # 왼쪽 탐색
postOrder(tree[now][1]) # 오른쪽 탐색
print(now,end='')
# 공백없이 출력
# 전위순회
preOrder('A')
print()
# 중위순회
inOrder('A')
print()
# 후위순위
postOrder('A')
전위순회는 현재 노드 출력 -> 왼쪽 노드 탐색 -> 오른쪽 노드, 중위 순회는 왼쪽 탐색 -> 현재 노드 출력 -> 오른쪽 노드 탐색, 후위 순위는 왼쪽 탐색 -> 오른쪽 탐색 -> 현재 노드 출력 순으로 구현하였습니다. 만약 .인 경우에는 노드가 없다는 뜻이므로 리턴값이 없습니다.
개발감자였습니다!
'알고리즘' 카테고리의 다른 글
| [알고리즘] 파이썬 기본 문법 정리 (2) | 2024.04.16 |
|---|---|
| 세그먼트 트리 개념 및 구현 / 코딩테스트 주요 5대 알고리즘 (0) | 2024.01.18 |
| [알고리즘 마스터] 14. 트리와 트라이 (0) | 2024.01.16 |
| [알고리즘 마스터] 13. 정수론 (소수, 오일러 피, 유클리드 호제) (1) | 2024.01.13 |
| [알고리즘 마스터] 12. 스택과 큐 (1) | 2024.01.08 |



